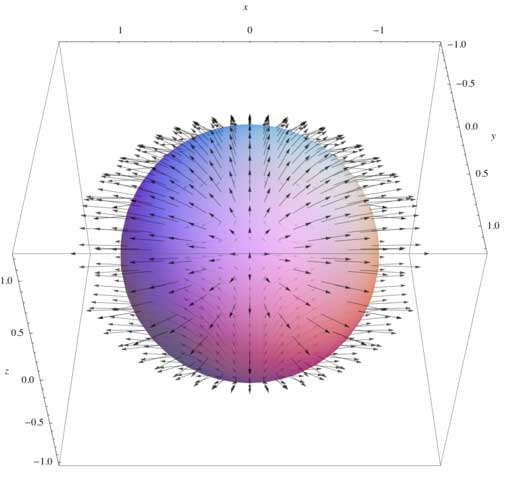
An electromagnetic field (also EMF or EM field) is a physical field produced by electrically charged objects. It affects the behavior of charged objects in the vicinity of the field.
- Just like that you are a person with some mass (or weight), let’s say 130 lbs (I’m sorry if you are much heavier than that), you will produce a gravity field and the sun will be dragged a little bit nearer to you. Actually the EMF works just like that, but a little bit different.
The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction. It is one of the four fundamental forces of nature (the others are gravitation, weak interaction and strong interaction). If you are interested in these forces especially the latter two, I highly recommend Dr.Leon Lederman’s book: The God Particle. While here we only focus our eyes on the EMF, and in classical physics: we just think the EMF as a smooth, continuous field.
The field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, and the magnetic field by moving charges (currents); these two are often described as the sources of the field. The way in which charges and currents interact with the electromagnetic field is described by Maxwell’s equations and the Lorentz force law. Actually the Maxwell’s equations are the destinations of this lesson here…
1. Vector Field: Flux && Circulation
What are we talking about when we talk about a vector field?
How can we describe a vector field in a visualized way?
“Field line.” Said Michael Faraday.

Faraday: See? those bits of iron around the bar magnet proved me right. :)
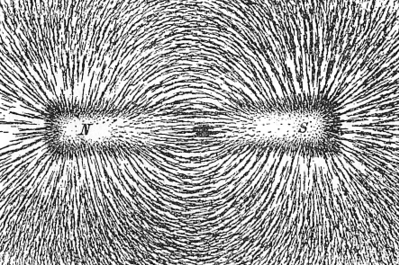
Very good indeed… but not precise enough. These visible lines are just a small part of the infinite lines excited by the sources of these fields. Maybe a more mathematical way is better.
Actually, if we classify these force lines, there are two kinds: one is divergent, the other is vortical.
In fact, when we are “measuring” a vector field, the proper mathematical way is exactly to “count” how “many” force lines are going through an infinitesimal surface ( flux ) && running along an infinitesimal closed curve ( circulation ).
Apparently, if we take physical truth into account, these infinitesimal surfaces and infinitesimal closed curves must have directions. For example, if our surface is a closed surface which surrounds the source of our field, say, a positive charge, so we have to orient the surface with a normal vector pointing always outwards. Another example: if our source is at the center of our closed curve, we have to use the almighty right-hand rule to judge the positive direction of our curve.
Here are the definitions: Let’s assume that we have a “spring water source”, the water is incompressible and its density is 1. The velocity field of the “spring water” is $\vec{v}(x,y,z)$, where: $$\vec{V}(x,y,z)=P(x,y,z)\vec{i}+Q(x,y,z)\vec{j}+R(x,y,z)\vec{k}$$
So:
Flux:
$$\begin{aligned}
\Phi=\int_{\Omega}\vec{V}d\vec{S}=\iint_{\Sigma}\vec{V}\cdot\vec{n}dS=\iint_{\Sigma}(Pcos\alpha + Qcos\beta + Rcos\gamma)dS
\end{aligned}$$
If $\Sigma$ is a closed surface and its normal outward vector’s direction is its positive direction, then:
$$\begin{aligned}
\Phi=\iint_{\Sigma}Pdydz+Qdzdx+Rdxdy
\end{aligned}$$
- If $\Phi>0$, then there is a equivalent positive source inside.
- If $\Phi<0$, then there is a equivalent negative source inside.
- If $\Phi=0$, then there is equivalently no source inside.
Circulation:
$$\begin{aligned}
\Gamma=\oint_{L}\vec{V}d\vec{l}=\oint_{L}\vec{V}\cdot\vec{\tau}ds=\oint_{L}(Pcos\lambda+Qcos\mu+Rcos\nu)ds
\end{aligned}$$
Now we can describe a vector field in integral form.
2. Vector Operators, Divergence && Curl
Now let’s think of differentiation.
Don’t you think vector field is a perfect stage for differentiation? Maybe differentiation was born for it, isn’t it Sir Newton?
According to Gauss’s theorem:
$$\begin{aligned}
\Phi=\iiint_{\Omega}(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dxdydz
\end{aligned}$$
If we shrink our surface $\Sigma$ until it becomes an infinitesimal point.
$$\begin{aligned}
\lim_{\Omega\to M}\frac{\Phi}{V}=\lim_{\Omega\to M}\frac{1}{V}\iiint_{\Omega}(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})dxdydz=(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})_{M}
\end{aligned}$$
This is the divergence of the vector field.
It’s a little bit too inconvenient to write something like $(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z})_{M}$, so we use a vector operator to rewrite these formulas.
$$\begin{aligned}
div\vec{V}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\nabla\cdot\vec{V}
\end{aligned}$$
Now let’s come to curl ( or vorticity ).
According to Stokes’ theorem:
$$\begin{aligned}
\Gamma=\iint_{\Sigma}(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z})dydz+(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x})dzdx+(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy
\end{aligned}$$
So, the vector $(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})$ is defined as the curl of the vector field.
It’s really hard to be memorized, isn’t it?

Fortunately we have already learned some linear algebra.
$$\begin{aligned}
& curl\vec{V}=(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})\\
& =
\left|\begin{array}{cccc}
\vec{i} & \vec{j} & \vec{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z}\\
P & Q & R
\end{array}\right|
=\nabla\times\vec{V}
\end{aligned}$$
WELL DONE :)
3. Scalar Field: Gradient
Now let’s look back to scalar field. Much easier aren’t they?
In fact, a scalar field is just like a mountain, different places ( coordinates ) have different heights ( coordinate values ). So if we are on the top of the mountain, what really matters to us is in which directions can we get the top speed to get down the mountain ( maybe rolling down the mountain :) ), and what is the speed?
Sir Issac Newton has told us how to get the answer: derivation!
Gradient:
$$\begin{aligned}
gradf=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}+\frac{\partial f}{\partial z}\vec{k}=\nabla f
\end{aligned}$$
4. Some Special Vector Fields && Helmholtz’s Theorem && Two Formulas
What would happen if the divergence or curl of a vector field equal to zero?
- If $\nabla\cdot\vec{V}=0$, there is no “diverging source” inside the field. Actually, no electric charges.
- If $\nabla\times\vec{V}=0$,then there is no “helical source” inside the field. Actually, no electric currents.
And Helmholtz’s theorem tells us why are these 3 values: gradient, divergence and curl, so important. Because arbitrary vector field $\vec{F}(\vec{r})$ can be described like this:
$$\begin{aligned}
\vec{F}(\vec{r})=-\nabla u(\vec{r})+\nabla\times\vec{A}(\vec{r})
\end{aligned}$$
Also, here are two important formulas:
$$\begin{aligned}
\nabla\times\nabla u = 0\\
\nabla\cdot(\nabla\times\vec{A})=0
\end{aligned}$$
You can understand these formulas by imagining the force lines.
5. Summary
- Integral form: flux, circulation;
- Differential form: divergence, curl, gradient.
Later, we will use these mathematical tools to analysis EMF.
BY THE WAY, the calculation formulas of gradient, curl and gradient above are just appropriate for rectangular coordinate system. In other system like spherical coordinate system or cylindrical coordinate system, the formulas are different.
References:
- Liu,Wenkai. Electromagnetic Fields and Electromagnetic Waves. [M]. Beijing: BUPT Press, 2013.
- Department of Mathematics, Tongji University, Advanced Mathematics, 6th ed. [M]. Beijing: Higher Education Press, 2007.
- Wikipedia [EB/OL]. https://en.wikipedia.org, 2016-02-09.